5.7 Kepler's Laws
(Discovering the Universe, 5th ed., §2-3)
- Although the heliocentric model worked just as well as the
geocentric model, to make it work over a millenium Copernicus
still had to add epicycles.

- The German astronomer Johannes
Kepler (1571-1630) had a different idea, however.
Kepler didn't believe planetary orbits were necessarily circles,
but could instead be other closed curves, such as the ellipse
or oval.
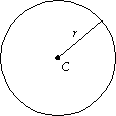
- Recall that a circle is defined as the set of all
points that are a constant distance r (the radius)
from the center C.
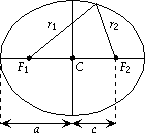
- An ellipse is a generalization of a circle, involving
two points F1 and F2(each called
a focus, and together the foci) and two distances
r1
and r2,
whose sum is a constant:
r1
+ r2
=2a
When the foci coincide (coming together at the center), the result
is a circle with a radius a.
- The constant 2a is equal to the length of the longer
or "major" axis, so a is called the semimajor
axis.
The semimajor axis therefore describes the overall size of the
ellipse.
It can be shown that a is the average distance of the
ellipse from one focus.
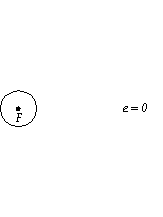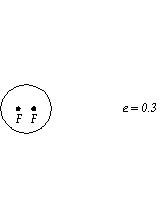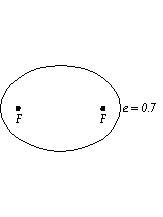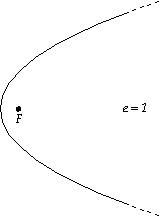 The constant c describes how far each focus is from the center, which determines how elongated the ellipse is (for a given value of a). The constant c describes how far each focus is from the center, which determines how elongated the ellipse is (for a given value of a).
However, it is more useful to use the eccentricity:
e = c/a
Because c is always less than a, the value
of e varies between 0 and 1.
When e = 0, c = 0, the foci coincide, and we have
a circle.
When e =1, the foci approach the opposite ends of the
ellipse; the result is so elongated that, from one focus, both
the center and the other focus are infinitely far away, forming
a curve called a parabola.
 Kepler
came to work with Tycho in 1600, and the latter's astronomical
records provided Kepler with the data he needed to test his hypothesis. Kepler
came to work with Tycho in 1600, and the latter's astronomical
records provided Kepler with the data he needed to test his hypothesis.
After many years of laborious calculations, Kepler was able to
demonstrate what is now known as Kepler's First Law:
Planetary orbits are ellipses, with the Sun at one focus.
- Because the Sun is off-center, we can describe two special
positions on a planet's orbit, both on the major axis:
The perihelion is the point of closest approach to the
Sun; it is a distance a(1 - e) from the Sun.
The aphelion is the point where the planet is farthest
from the Sun; it is a distance a(1 + e) from the
Sun.
- As can be seen in the table at the right, the eccentricity
of the planets' orbits is generally quite small, except for Mercury
and Pluto, whose orbits are noticeably elongated.
This is why circles initially worked well in describing planetary
orbits.
- The table also shows the orbital inclination, or tilt,
of the planets' orbits relative to the ecliptic plane.
|
| Planet |
Semimajor
Axis a |
Sidereal
Period P |
Eccen-
tricity e |
Orbital
Inclination |
| Mercury |
0.3871 AU |
0.2408 y |
0.206 |
7.00° |
| Venus |
0.7233 AU |
0.6152 y |
0.007 |
3.39° |
| Earth |
1.0000 AU |
1.0000 y |
0.017 |
0.00° |
| Mars |
1.5237 AU |
1.8809 y |
0.093 |
1.85° |
| Jupiter |
5.2028 AU |
11.862 y |
0.048 |
1.31° |
| Saturn |
9.5388 AU |
29.458 y |
0.056 |
2.49° |
| Uranus |
19.1914 AU |
84.01 y |
0.046 |
0.77° |
| Neptune |
30.0611 AU |
164.79 y |
0.010 |
1.77° |
| Pluto |
39.5294 AU |
248.5 y |
0.248 |
17.15° |
|
The orbital inclination is usually quite small, except for
Pluto.
Question: where did we
see orbital inclination previously?
Question: why doesn't
a planet usually disappear behind the Sun when they are in conjunction?
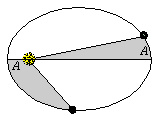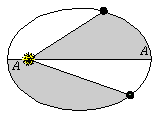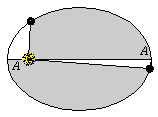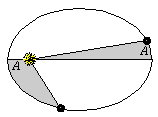 Kepler also noticed
another characteristic of planetary motion: planets move fastest
at perihelion, and slowest at aphelion. Kepler also noticed
another characteristic of planetary motion: planets move fastest
at perihelion, and slowest at aphelion.
Kepler was able to quantify these varying speeds in what is known
as Kepler's Second Law:
Planets sweep out equal areas in equal times.
- Kepler published his First and Second Laws in 1609 in a book
entitled New Astronomy.
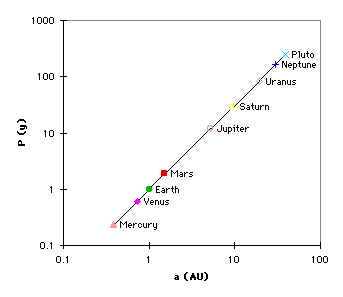
- Ten years later, in 1619, Kepler discovered and published
an additional relationship.
Kepler's Third Law quantifies the observation that more
distant orbits have longer periods:
a3
= P2
Here, the semimajor axis a is measured in A.U. and the
orbital period P is measured in years.
The graph at the right shows log P vs. log a; the
data falls along a straight line, with a slope of 3/2.
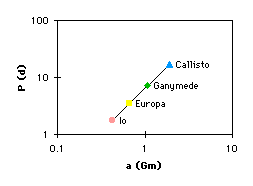
- Kepler also noticed that the Galilean satellites obeyed the
Third Law, as can be seen by the same 3/2 slope in the graph
at the right.
This implied that Kepler's Third Law was a general principle.
- Galileo himself refused to accept Kepler's ideas, clinging
to the notion that planetary orbits must be circular, though
his reasons were based on his studies of motion rather than on
tradition.
|