6.11 Confirmations of Newton's Laws
(Discovering the Universe, 5th ed., §)
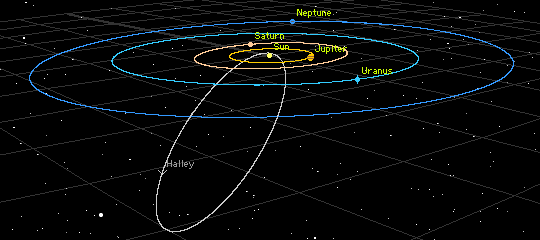
 A contemporary
of Newton, Edmond Halley (1656-1742), had been studying comets, bright objects
that appear briefly in the sky from time to time and move relative
to the stars, like planets (though much faster). A contemporary
of Newton, Edmond Halley (1656-1742), had been studying comets, bright objects
that appear briefly in the sky from time to time and move relative
to the stars, like planets (though much faster).
Halley noticed that the comets of 1531, 1607, and 1682 had similar
characteristics, and were separated by the same period of 76
years.
In 1684, Halley visited Newton in Cambridge, and told him about
his suspicion that they were the same comet moving in
a periodic orbit around the Sun.
It was only then that Halley learned of Newton's unpublished
work on planetary motion.
Newton advised Halley that the comet's orbit must be elliptical,
though much more elongated than a planet's.
Photo Information

- Halley applied Newton's laws to correctly predict the date and location of the
comet's reappearance in 1758.
That comet is now known as Halley's Comet; its most recent passage was in 1986.
Halley's comet has an orbit with an eccentricity of 0.9673 and
a semimajor axis of 17.9 AU (its aphelion of 35.3 AU takes it
out beyond the planet Neptune!).
- It wasn't long before astronomers had applied Newton's Laws to determine the masses of the known planets, by observing their interaction with their moons and with each other.
 In 1781, an
amateur astronomer named William
Herschel, who had built one of the most powerful telescopes
of the time, noticed "a curious either nebulous star or
perhaps a comet". In 1781, an
amateur astronomer named William
Herschel, who had built one of the most powerful telescopes
of the time, noticed "a curious either nebulous star or
perhaps a comet".
Subsequent observations revealed that this object moved relative
to the stars, although more slowly than a comet.
Herschel soon realized that he had discovered a seventh planet,
Uranus (and the first in recorded history!).
At its brightest, Uranus is barely visible to the naked eye in a dark sky.
Because of its slow motion, however, Uranus was always mistaken for a star by earlier observers.
 Uranus
has an orbital period of 84 years, but after 50 years it was
clear that it wasn't following its predicted orbit. Uranus
has an orbital period of 84 years, but after 50 years it was
clear that it wasn't following its predicted orbit.
Astronomers applied Newton's Laws to account for the gravitational
pulls of Jupiter and Saturn, but that still did not remove all
of the discrepancies.
John
Couch Adams and Urbain-Jean-Joseph
Le Verrier independently realized that a new planet beyond
Uranus might cause these deviations.
In 1843 and 1845, respectively, they applied Newton's Laws to
determine its position.
In 1846 Galle and d'Arrest at the Berlin Observatory followed
up on Le Verrier's prediction, and quickly identified the eighth
planet, Neptune.
Neptune moves even more slowly than Uranus, and it has an orbital
period of 165 years.
Question: in the picture
shown, looking down on the solar system, what effect would the
gravity of the outer planet (Neptune) have on the speed of the
inner planet (Uranus)?
- After some years, positional errors in Neptune's predicted
orbit again suggested the presence of another large planet further
out.
In 1905, another amateur astronomer, Percival
Lowell, who had built his own observatory in Arizona, began
a search for this planet, which he called Planet X.
After Lowell died in 1916, his successors at the Lowell
Observatory continued the search.
Finally, in 1930, Clyde
Tombaugh discovered Pluto, but its observation was
fortuitous because its mass is so small that it doesn't have
a significant effect on Neptune.
Better measurements of the outer planets' masses (by the Voyager
spacecraft in 1970s and 1980s) have now removed the errors in
Neptune's position.
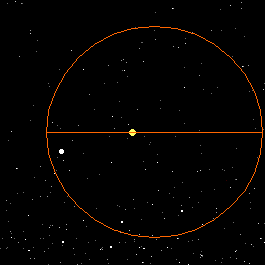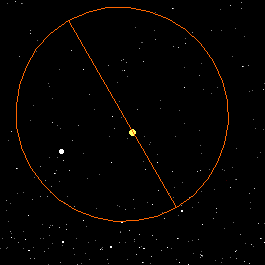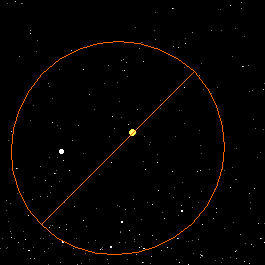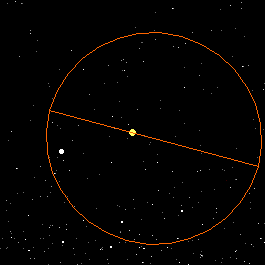 Generally
speaking, a planetary orbit should be fixed in space. Generally
speaking, a planetary orbit should be fixed in space.
Question: what physical principle
requires this?
However, another planet's gravitational pull can make a planet's
orbit precess around the Sun.
Question: where have we already
seen an example of a precessing orbit?
In 1845, Le Verrier discovered that Mercury's orbit also precesses
around the Sun (note the changing orientation of the semimajor
axis in the picture).
This is a very small effect, only 0.10 seconds of arc
per orbit (43" per century), but even so it could not be
explained by the other planets.
Le Verrier hypothesized that there might be another planet inside
of Mercury's orbit, so close to the Sun that it was difficult
to observe.
This planet, which Le Verrier called Vulcan, has never
been found.
So, there was no good explanation for Mercury's precession using
Newton's laws, but, like Neptune, the effect was small enough
to attribute to measurement errors, and was largely ignored.
|