Lecture 9: The Speed of Light and Relativity

The lights of stars that were extinguished ages ago still reaches us. So it is with great men who died centuries ago, but still reach us with the radiations of their personalities.

-- Kahlil Gibran

9.1 The Speed of Light

(Discovering the Universe, 5th ed., §3.1)

• Everything we know about the stars and other objects in the universe comes to us through their release of some form of light, both visible and invisible.
  
  It is therefore important to understand light's basic properties to determine what that reveals about the stars.
  
   
  
• Although light appears to travel instantaneously from its emission to its detection, it does in fact have a finite speed, which must be very, very fast.
  
   
  
• The first person known to attempt a determination of the speed of light was Galileo.
  
  Galileo and an assistant each took a shrouded lantern and stood within site of each other on two widely-separated hilltops.
  
  Galileo opened his lantern, and when the assistant saw its light, he opened his, too.
  
  Galileo measured the time it took from when he opened his lantern to when he saw his assistant's lamp, which should be the time for light to travel back and forth between the two hilltops.
  
  Question: how would this information be used to determine light's speed?
  
  Unfortunately the time Galileo measured could not be distinguished from the time it took to open the lanterns, again due to light's high speed.
  
   
  
• The first determination of the speed of light was an astronomical one, since only in this circumstance will large distances result in a measurable travel time.
  
  In 1676, the Danish astronomer Ole Rømer (1644-1710) was studying the orbits of Jupiter's Galilean satellites.
  
  Over a period of many months, Rømer recorded the starting time of eclipses of these moons by Jupiter.
  
  These eclipses should occur periodically, so the nth eclipse should begin after a time nP.
  
  For example, the closest moon Io has an orbital period of P = 42.5 h, so the second eclipse takes place after 2P = 85.0 h, the third after 3P = 127.5 h, etc.
  
  However, after a time equal to half of Jupiter's synodic period, the eclipses were occuring after a time nP + 16.6 minutes!
  
  And after another half synodic period, the variation had disappeared, and the eclipses were again occuring after an integral number of periods.
  
  This correlation with the relative position of Earth and Jupiter could only be due to the variation in their distance as they orbited the Sun.
  
  Rømer realized that if light had a finite speed, the time to travel over an extra distance of two astronomical units would explain the variation.
  
  The speed of light must then be:
  
  c = D/t = 2 AU/16.6 min = 7.2 AU/h
  
  The size of the astronomical unit wasn't determined until the 19th century, but once it was the speed of light could be expressed in terrestrial units:
  
  c = 2.998 x 10⁵ Km/s
  
  Note the use of the special symbol c for the speed of light.
  
   
  
• By the middle of the 19th century improved technology allowed the measurement of the speed of light in the laboratory, verifying this value.

9.2 The Constancy of the Speed of Light

(Discovering the Universe, 5th ed., §3.1, §13.1)

• One prediction of Newtonian physics is that the speed of light c should depend on the speed of its source v.
  
  If light is emitted in the same direction that the source is moving, it should travel faster, at a speed c + v.
  
  If light is emitted in the direction opposite to the motion of the source, it should travel slower, at a speed c - v.
  
   
  
• But there was a problem: a series of precise experiments in the 1880s found that the speed of light was always the same, no matter how fast or in what direction the source was moving!
  
   
  
• Although physics is rooted in the scientific method, this conflict between experiment and an otherwise well-founded theory was very difficult for physicists to overcome.

9.3 The Special Theory of Relativity

(Discovering the Universe, 5th ed., §13.1)

• While working in the Swiss Patent Office, Albert Einstein (1879-1955) developed what is now known as the Special Theory of Relativity, published in 1905.
  
  Einstein began with the experimental observation that light always has the same speed, and developed a number of unusual consequences:
  

1. The faster an object moves, the shorter it becomes.
   
   This length contraction is given by
   
   .
   
   The Lorentz factor
   
   
   
   is equal to 1 when the object isn't moving (v = 0) and approaches infinity as the object accelerates towards the speed of light (v -> c).
   
    
   
2. The faster a clock moves, the slower it runs.
   
   In other words, events in a moving system take longer to occur from the perspective of a system at rest.
   
   This time dilation is given by
   
   .
   
   In the picture on the right, the stopwatch in motion measures a five-second event, while the stopwatch at rest has seen 6 seconds pass.
   
    
   
3. The faster an object moves, the more massive it becomes.
   
   This mass increase is given by
   
   .
   
   Question: how might one measure this mass increase?
   
   An important consequence of mass increase is a violation of the principle of conservation of mass.
   
    
   
4. Mass can be converted into energy and vice versa.
   
   In addition to the violation of mass conservation above, it can be shown that conservation of energy is violated, i.e. the energy you put into accelerating an object doesn't all show up as the object's energy.
   
   But both the missing energy and the increased mass can be explained if you allow mass to be a form of energy, according to the following relation:
   
   E = mc²
   
   Note that, because c is so large, mass is a very, very concentrated form of energy.
   
   This generalized principle of conservation of mass + energy has profound consequences, as we will see later.
   
    
   
5. Nothing can travel faster than light.
   
   If you are accelerating an object towards the speed of light, its mass increases without bound, making it harder and harder to increase its speed.
   
   As a consequence, a massive object must always travel at less than the speed of light.
   
   Since light itself travels at the speed of light, it must have no mass!
   
    
   
6. Newton's Laws of Motion are approximations to Special Relativity that are applicable only at low speeds.
   
   In other words, Special Relativity is a generalization of Newton's Laws of Motion.
   
   In practice, one must be traveling faster than ~0.1c (30,000 Km/s!) to observe these special relativistic effects.
   
   Nevertheless, with sensitive experimental equipment such as atomic clocks, the predictions of Special Relativity have been verified to high precision.
   
    
   

• Extra: C-ship provides movies to help you visualize the effects of special relativity at high speeds.

9.4 The General Theory of Relativity

(Discovering the Universe, 5th ed., §13.2)

• The equivalence of mass and energy soon led Einstein to develop the General Theory of Relativity, published in 1916.
  
  Light has no mass, but it does have energy, so it should be affected by the presence of massive objects such as the Sun, just as the planets are.
  
   
  
• The General Theory of Relativity is based on a four-dimensional geometric framework of space and time called space-time.
  
  Space-time is not an emptiness, but instead has a physical presence that is affected by its contents.
  
  The predictions of General Relativity include:
  

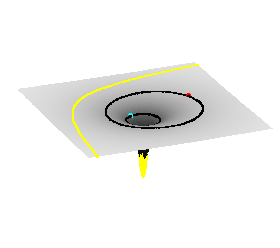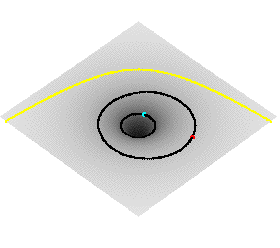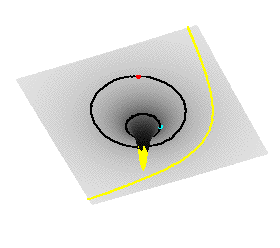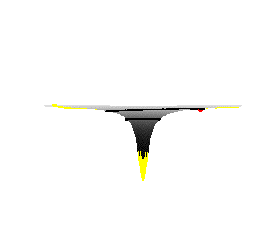1. The presence of mass or energy will curve space.
   
   You can think of space as a three-dimensional "rubber sheet" that is usually flat.
   
   But when a mass is placed on this "rubber sheet", it stretches and curves in response.
   
   When space is curved, a moving object must follow the curvature, i.e. change its speed and direction, just as a car must turn when the highway curves.
   
   
   Curvature of space thereby replaces Newton's concept of force as a means to accelerate objects.
   
   The gravity well takes on a new physical meaning, with the massive Sun sitting at its bottom, and the planets forced to curve around the walls of the well.
   
   Light must also curve around a massive object such as the Sun (see the yellow line in the picture above).
   
   Question: what shape will light's path have?
   
   The deflection of light near the Sun was verified during the solar eclipse of 1919, when a star that should have been invisible behind the eclipsed Sun could be seen.
   
   The observed amount of deflection, 1.75 arc sec, is the same as that predicted by General Relativity.
   
    
   
2. The presence of mass or energy will slow down time.
   
   In other words, clocks run more slowly near a massive object, another form of time dilation.
   
   Atomic clocks can detect a time difference between the bottom and top of a tall building!
   
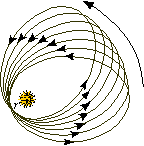   Time dilation near the Sun explains why Mercury's orbit precesses.
   
   Recall that angular momentum is given by
   
   AM ~ mr²/P
   
   AM is a conserved quantity, and the perihelion distance r doesn't change, either.
   
   So P, the time per orbit, must also be fixed.
   
   But time must dilate in the vicinity of the Sun, which means the orbit must become longer, i.e. the perihelion shifts its position in the direction of motion.
   
   The observed amount of perihelion shift, 43 arc sec/century, is the same as that predicted by General Relativity.
   
    
   
3. Newton's Laws of Motion and Law of Gravitation are approximations to General Relativity that are only applicable away from large masses or other concentrations of energy.
   
   In other words, General Relativity is a generalization of Newton's Laws of Motion and Gravitation.
   
   In practice, one must have an escape velocity faster than ~0.1c to observe these general relativistic effects.
   
   Nevertheless, with sensitive experimental equipment such as atomic clocks, the predictions of General Relativity have been verified to high precision.

The Gateway to Educational Materials (GEM) is the key to one-stop, any-stop access to thousands of high quality lesson plans, curriculum units and other education resources on the Internet! GEM is a project of the U.S. Department of Education. The Introduction to Astronomy Webbook is catalogued in the Gateway, and Scott R. Anderson is a member of the GEM Consortium.