|
Astronomy as a science began tens of thousands of years ago by tracking the motion of the Sun, Moon, planets, and stars.
It has since developed into a sophisticated study of the fundamental laws of nature governing these phenomena.
1.2 The Scientific Method
The scientific method ensures that astronomy is based on accurate, reproduceable theories.
1.3 Numbers, Numbers, Everywhere
(Discovering the Universe, 5th ed., §I-2)
- Comparisons of different astronomical objects require the use of numbers, e.g. which is bigger, the Earth or the Sun?
- To describe the wide range of values that show up in astronomy, power-of-ten notation is used:
1012 = 1,000,000,000,000 = trillion = tera = T
109 = 1,000,000,000 = billion = giga = G (commonly pronounced with both hard and soft "g")
106 = 1,000,000 = million = mega = M
103 = 1000 = thousand = kilo = K (officially lower case)
102 = 100 = hundred
101 = 10 = ten
100 = 1
- The exponent means that you are multiplying 10 together that many times, e.g.
103 = 10 x 10 x 10 = 1000.
- A simple rule to determine the exponent is to count the number of zeros.
- The abbreviations on the right are simpler to use and are therefore very common.
- Continuing to fractional powers of 10, negative exponents are used:
10-1 = 0.1 = tenth
10-2 = 0.01 = hundredth = centi = c
10-3 = 0.001 = thousandth = milli = m
10-6 = 0.000001 = millionth = micro = µ (Greek letter mu)
10-9 = 0.000000001 = billionth = nano = n
10-12 = 0.000000000001 = trillionth = pico = p
- A simple rule to determine a negative exponent is to count the number of places to the right of the decimal point, up to and including the first non-zero digit.
- Numbers in between the powers of ten, e.g. 5237, can be written more compactly as 5.237 x 103, and even more simply as 5.237 K.
This format is formally known as scientific notation.
- Generally each subsequent non-zero digit in a number is less "well-known" or precise because it is harder to measure.
Therefore, we will usually not specify more than 2 or 3 digits.
1.4 Physical Quantities
(Discovering the Universe, 5th ed., §I-2)
- We will be using several fundamental physical quantities in this class:
- Angle
- Distance or length
- Time
- Mass: a characteristic of an object which partially defines the force of gravity it feels (its weight).
Mass also describes an object's resistance to a change in its motion (inertia).
Mass is always positive or zero.
Conservation of mass is a fundamental law of nature; it can neither be created or destroyed.
Note that weight and mass are not the same!
An object with mass only has weight if another object (e.g. a planet) is nearby to provide a gravitational field.
So, for example, your weight on the Moon is only 1/6 of what it is on the Earth, but your mass is the same.
- Electric Charge: a characteristic of an object which partially defines the forces of electricity and magnetism it feels.
Benjamin Franklin performed many experiments in electricity, and he discovered that electric charge can be positive, zero, or negative.
Conservation of electric charge is also a fundamental law of nature; the total amount is zero, so if you find some positive charge somewhere, there must be an equal amount of negative charge somewhere else!
In nature there is a fundamental electric charge (e), which is characteristic of atomic particles, and all other charges are an integer multiple of that value.
For example, the electron has charge -e, and the proton has charge +e (per Franklin's arbitrary choice).
Question: What is the charge of the neutron?
- We will also be using many other quantities which depend on the above, e.g.
- Volume: length x length x length
- Density: mass/volume
- Speed: distance/time
- Electric Current (the flow of electric charge): electric charge/time.
1.5 Units
(Discovering the Universe, 5th ed., §I-2)
- Each of these physical quantities are described by one or more units, which are all related to each other by some conversion factor:
|
|
1 revolution = 360 degrees = 2 pi radians |
|
|
1 meter = 1.094 yard |
| |
1 yard = 3 feet |
| |
1 foot = 12 inches |
| |
1 mile = 5280 feet |
|
|
1 minute = 60 seconds |
| |
1 hour = 60 minutes |
| |
1 day = 24 hours |
| |
1 year = 365.25 days |
|
|
gram = the mass of 10-6 cubic meters of water
(one teaspoon has about 5 grams of water) |
|
|
e |
| |
1 Ampere-hour = 2.25 x 1022 e
(a D-cell battery provides about 3 Ampere-hours) |
- Rather than electric charge, you are probably more familiar with:
|
|
Ampere = 6.24 x 1018 e/second |
- As in all sciences, we will use the International System (commonly known as the metric system), a precisely defined set of units maintained by the International Bureau of Weights and Measures in Sèvres, France.
The fundamental units are meter for length, second for time, gram for mass, and Ampere for electric current.
In physics, the kilogram (1000 grams) is more commonly used.
- All units have standard abbreviations, which we will use regularly:
|
|
revolution = rev |
| |
degree = ° |
|
|
second = s = " |
| |
minute = min = ' |
| |
hour = h |
| |
day = d |
| |
year = y |
- Combined with the previous numeric abbreviations we have a very flexible, compact notation for describing physical quantities:
kilometer = Km = 1000 m (~5/8 mile)
centimeter = cm = 0.01 m (1 inch = 2.54 cm by U.S. law)
kilogram = Kg = 1000 g (1 Kg has a weight on Earth of 2.2 pounds)
gigayear = Gy = 109 y (age of the universe ~13 Gy)
milliAmpere = mA = 10-3 A (common current used by electronic equipment)
megabyte = MB = 106 B (a byte is the computer memory required to hold one character)
- Note the symbol ~, which means "about" or "approximately"
- Let's consider some astronomical distances:
| Earth's Radius |
6.4 x 103 Km
= 6.4 Mm |
|
|
| Earth-Moon |
3.8 x 105 Km
= 380 Mm |
2.5 x 10-3 AU
= 2.5 mAU |
|
| Earth-Sun |
1.5 x 108 Km
= 150 Gm |
1 AU |
8.3 lmin |
| Sun-Pluto |
5.9 x 109 Km
= 5900 Gm
= 5.9 Tm |
39 AU |
324 lmin
= 6.2 x 10-4 ly |
| Sun-Nearest Star |
4.0 x 1013 Km |
2.7 x 105 AU |
4.2 ly |
| Sun-Center of Galaxy |
2.6 x 1017 Km |
|
2.8 x 104 ly
= 28 Kly |
| Nearest Comparable Galaxy (Andromeda) |
2.1 x 1019 Km |
|
2.2 x 106 ly
= 2.2 Mly |
| Farthest we can see |
~1.2 x 1023 Km |
|
~1.3 x 1010 ly
= 13 Gly |
- A more useful measure for interplanetary distances is the astronomical unit (abbreviated AU), defined as the average distance between the Earth and the Sun:
1 AU = 1.496 x 108 Km
- For interstellar distances, it is easiest to use the light year (abbreviated ly), defined as the distance that light travels in one year:
1 ly = 9.46 x 1012 Km = 6.32 x 104 AU
For galactic and intergalactic distances, astronomers use Kly and Mly, respectively.
- Within the solar system, it is also possible to use the light minute:
1 lmin = 1.80 x 107 Km = 0.120 AU
- Extra: a visual representation of distance powers-of-10 can be observed at the National High Magnetic Field Laboratory (requires Java). Thanks to former Emory student Mindy Tabin for bringing this to my attention!
1.6 Angular Measurement
(Discovering the Universe, 5th ed., §I-2)
- For observational astronomy, a common tool is angular measurement, which describes the apparent size of an object (angular diameter), or the apparent distance between two objects (angular separation), as viewed from the Earth:
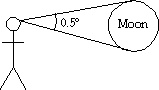 For example, the Moon has an angular diameter of 1/2°. For example, the Moon has an angular diameter of 1/2°.
We say that the Moon subtends 1/2°.
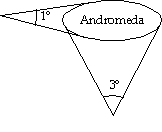 The Andromeda Galaxy is even larger than the Moon; it subtends angles of 1° by 3°: The Andromeda Galaxy is even larger than the Moon; it subtends angles of 1° by 3°:
- When objects are magnified in a telescope, the field of view (the portion of the sky we can see) gets smaller and smaller.
Therefore, small angular sizes are very common.
To talk about fractions of a degree, astronomers use the minute of arc and the second of arc:
1° = 60 arc min = 60'
1' = 60 arc sec = 60"
Note that this is the same relation to the degree that minutes and seconds have to the hour.
So, the Moon subtends 30'.
- Note that angular measurement depends on how far away something is!
So, Venus will have a wide range of angular diameters because its distance from the Earth is constantly varying:
Venus closest: 1.0' = 60"
Venus farthest: 0.16' = 9.7"
- Similarly, the Moon's distance changes, so it has an angular diameter between 32.7' (closest) and 29.6' (farthest), and the Sun varies between 32.5' (closest) and 31.5' (farthest).
Question: What would happen if the Moon passed in front of the Sun?
- Stars are so far away that they have angular diameters of zero, i.e. they are point objects.
1.7 The Parsec
(Discovering the Universe, 5th ed., §I-2)
- Angular measurement can be used to define yet another measure of linear distance, which arises naturally out of observational astronomy.
An angle a is related to the arc length s it subtends along a circle and the radius r of the circle:
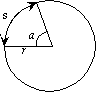 Obviously, the larger the angle a is, the larger s will be. Obviously, the larger the angle a is, the larger s will be.
The exact relationship is
s = kra
where k is a constant that depends on the units used (e.g. if a is measured in radians and s and r are measured in the same units, then k = 1).
- When the Earth moves in its orbit, nearby stars can be observed to move against the static background of far-away stars.
This apparent motion of an object due to the motion of the observer is known as parallax.
You are familiar with parallax from riding in a car: trees outside appear to move past you when in fact it is you that moves.
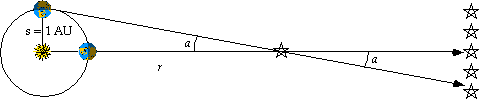
Extra: an animation of stellar parallax can be observed at Cornell University (requires Java).
- The angular change a in the position of a star when the Earth moves depends on how far away it is; the further it is, the smaller the parallax.
Comparing with the previous picture of a circle, we can see that there is a simple relation between the distance to the star r, the angle of parallax a, and the distance through which the Earth moves s:
r = s/ka
If s is measured in AU, a is measured in seconds of arc, and k is set to 1, then
r = 1 AU/a ,
and r is a unit called a parsec (abbreviated pc).
So, if a star exhibits a maximum parallax of one second of arc when the Earth has moved through 1 AU, it is one parsec away.
Question: In three months time, the star Krüger 60 exhibits a maximum parallax of 1/4 arc sec. How far away is it?
Even if one doesn't know what an AU is (and for a long time no one did), the parsec can still be used to describe the relative distance to nearby stars.
Once the value of the AU was determined, it could be calculated that 1 pc = 3.26 ly.
|